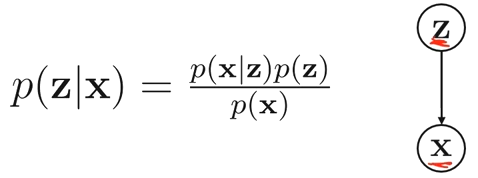深度学习：深度生成模型

判别式模型和生成式模型
- 判别式：学习类别的边界（比如CNN、RNN）
- 生成式：学习数据的分布（VAE、GAN）。比判别式更加复杂

蒙特卡洛方法

采样 sampling

采样可以减少积分运算量（尤其是概率密度函数特别复杂的时候，可能无法求出解析解），便于统计推断和模型优化。
蒙特卡洛采样：从概率分布中抽出样本，得到分布的近似。样本越多，近似的越准

公式详解： $s = \int p (x) f (x) d x = E_{p} [f (x)]$ 是一个积分形式的期望表达式。其中 $p (x)$ 是概率密度函数（当 $x$ 是连续型随机变量时）， $f (x)$ 是关于随机变量 $x$ 的函数。 $\int p (x) f (x) d x$ 表示对 $f (x)$ 关于概率分布p $(x)$ 求积分，得到的结果 $s$ 就是函数 $f (x)$ 关于分布 $p (x)$ 的期望 $E_{p} [f (x)]$ 。在概率论和统计学中，期望是随机变量取值的加权平均，这里的权重就是概率密度 $p (x)$ 。

${\hat{s}}_{n} = \frac{1}{n} \sum_{i = 1}^{n} f (x^{(i)})$ 是蒙特卡罗估计的形式。这里$ \boldsymbol{x}^{(i)} $是从分布$ p(\boldsymbol{x})$中抽取的第 $i$ 个样本， $n$ 是样本数量。通过抽取 $n$ 个样本，计算 $f (x)$ 在这些样本上的取值并求平均，来近似上方公式中的期望 $E_{p} [f (x)]$ 。随着 $n$ 增大，根据大数定律， ${\hat{s}}_{n}$ 会依概率收敛到 $E_{p} [f (x)]$ ，即 $l i m_{n \to \infty} {\hat{s}}_{n} = E_{p} [f (x)]$ 。蒙特卡罗方法常用于==难以直接计算积分（期望）==的情况，通过采样和平均来获得近似解。

可以看出，随着采样数的增加，采样的精准度越来越好。在1000个样本的时候，拟合出的曲线更接近 $p (x)$

Importance Sampling

用于估计难以采样的分布的期望值。举例来看就是 $f (x)$ 在 $p (x)$ 中的分布可能不是很均匀，在 $f (x)$ 取值很小的时候在 $p (x)$ 中的概率很大，而 $f (x)$ 取值很大的时候在 $p (x)$ 中的概率很小，这就会让期望的计算难以收敛。
用易于采样的参考分布生成样本，然后用权重系数调整估计

此处 $p (x)$ 不好采样，就用如高斯分布等更为简单的 $q (x)$ 来近似

马尔科夫链蒙特卡洛方法

Markov Chain Monte Carlo (MCMC)
一种动态的采样方法。
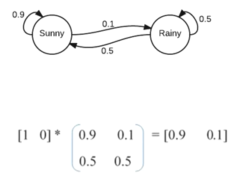
- 使用状态转移矩阵，从起始状态开始，转移出一系列的状态，这一系列的状态就是最后的采样结果
状态与转移：图中有两个状态“Sunny（晴天）”和“Rainy（雨天）” 。状态之间的带箭头连线和数字表示状态转移概率。比如从“Sunny”状态到自身的转移概率是(0.9)，意味着晴天后还是晴天的概率为(0.9)；从“Sunny”到“Rainy”的转移概率是(0.1) ，即晴天转雨天概率为(0.1) ；从“Rainy”到“Sunny”概率是(0.5)，“Rainy”到自身概率是(0.5) 。

状态转移矩阵：图中下方的矩阵 $[\begin{matrix} 0.9 & 0.1 \\ 0.5 & 0.5 \end{matrix}]$ 就是该马尔可夫链的状态转移矩阵，矩阵的行和列分别对应“Sunny”和“Rainy”状态，矩阵元素 $p_{i j}$ 表示从状态 $i$ 转移到状态 $j$ 的概率。

::: tips
提示
马尔可夫链的核心特性是无后效性，即系统在某个时刻的状态转移只取决于当前状态，与过去状态无关。
:::
好处：不用在整个分布空间中均匀采样，可以进一步提升采样的效率

变分推断（Variational Inference）

参数估计

机器学习的本质：从已有数据中估计出参数
- 求解过程：最优化理论
两个学派：
- 第一个学派（频率学派）认为，数据就是客观存在的，不受任何影响，所以直接求 $p (x | z)$ ，即先验概率（在给定参数 $z$ 的前提下，数据为 $x$ 的概率）。
  
  频率学派重点关注基于已有数据对总体参数进行估计。比如估计一枚硬币正面朝上的概率，通过大量抛硬币试验，用正面朝上的频率近似这个概率，不考虑其他潜在 “隐变量” 。他们认为存在一个真实固定的参数值，通过足够多数据和合适统计方法就能逼近这个真值。
  
  常用方法有最大似然估计(MLE)（ $L (θ | x) = P (X = x | θ)$ ）。最大似然估计根据样本构造似然函数，找到使似然函数最大的参数值，认为这就是对总体真实参数的最佳估计，强调数据本身对参数估计的作用，不依赖先验信息。
- 第二个学派（贝叶斯学派）认为，观测到的数据 $x$ 会受到隐变量 $z$ 的影响，所以他们求的是后验概率 $p (z | x)$ 。
  
  基于贝叶斯定理，后验概率 $p (θ | x)$ 可以表示为 $p (θ | x) = \frac{p (x | θ) p (θ)}{p (x)}$ ，其中 $θ$ 是待估计的参数， $x$ 是观测数据。 $p (x | θ)$ 是似然函数，表示在给定参数 $θ$ 下观测到数据 $x$ 的概率； $p (θ)$ 是先验概率，反映了在观测数据之前对参数 $θ$ 的认知； $p (x)$ 是证据因子，通常作为归一化常数.
  
  最大后验估计就是找到使后验概率 $p (θ | x)$ 最大的参数 $θ$ 值，即 ${\hat{θ}}_{M A P} = \arg max_{θ} p (θ | x) = \arg max_{θ} \frac{p (x | θ) p (θ)}{p (x)}$ 。由于 $p (x)$ 与 $θ$ 无关，所以等价于 ${\hat{θ}}_{M A P} = \arg max_{θ} p (x | θ) p (θ)$ 。
  
  与最大似然估计的比较：
  - 最大似然估计：只考虑似然函数 $p (x | θ)$ ，通过找到使 $p (x | θ)$ 最大的 $θ$ 值来估计参数，没有利用先验信息。当数据量足够大时，最大似然估计能得到较好的结果，但在数据量较少时，可能会出现过拟合或不合理的估计。
  - 最大后验估计：综合了似然函数和先验概率，在数据量较少时，先验信息可以起到正则化的作用，帮助避免过拟合，得到更符合实际情况的估计结果。例如，在估计一个硬币正面朝上的概率时，如果没有先验信息，最大似然估计可能会根据少量的投掷结果给出一个极端的估计值。但如果有一个合理的先验，如认为硬币大致是均匀的，那么最大后验估计会在似然函数和先验之间进行平衡，得到一个更合理的估计。
  ::: success
  思考
  
  感觉贝叶斯学派更屌一些？毕竟人家是直接从当前的数据中直接推算出来了针对当前数据的一组参数。
  
  :::

通过两个学派的讲解，其实对当前的深度学习可以进行一个分类。对于传统的深度神经网络（如CNN、RNN等）或者称判别式模型，都是基于频率学派的。其是通过最优化理论找到一组参数来尽可能使结果逼近真值。而概率生成模型，都是基于贝叶斯学派的。

求解最大后验估计

p (z | x) = \frac{p (x | z) p (z)}{p (x)} = \frac{p (x | z) p (z)}{\int p (z) p (x | z) d z}

其中 $p (x | z)$ 是似然函数(likelihood)， $p (z)$ 是先验(prior)， $p (x)$ 是evidence。evidence使用积分来求解，但是其很多时候都是一个不可积的积分，无法获得解析解。这时候可以使用马尔科夫链蒙特卡洛方法（MCMC）来取样，近似的求解 $p (z | x)$ 。

但是MCMC方法计算较慢，变分推断更适合求解大规模推断，适合并行计算。

变分推断的算法思路

图中黄色的部分就是要求的目标分布（ $p (z | x; ϕ)$ ， $φ$ 是参数）,红色的曲线 $q (z; θ)$ （可以是一个已知的高斯分布， $θ$ 是参数）是用来近似目标分布的。现在只需要移动曲线 $q$ ，使其尽可能多的与黄色部分重叠。绿色曲线代表了最后重叠最大的位置。

上面的描述是定性的，用定量的数学语言来描述就是最小化两个分布之间的KL散度，具体公式如下：

min_{θ} K L (q (z; θ) | | p (z | x; ϕ))

目标就是求出一个参数 $θ$ ，也就是怎么移动 $q$ 。

KL散度
- 概念：用于衡量两个分布之间的距离，是一种相对熵
- 相对熵 = 交叉熵 - 信息熵
- 计算公式：
  $K L (q (z; θ) | | p (z | x))] = E_{q (z; θ)} [\log \frac{q (z; θ)}{p (z | x)}]$
  是针对假定的函数 $q$ 来求期望。
公式推导
$\begin{aligned} K L (q (z; θ) | | p (z | x))] \\ = & E_{q} [\log \frac{q (z)}{p (z | x)}] \\ = & E_{q} [\log q (z) - \log p (z | x)] \\ = & E_{q} [\log q (z) - \log \frac{p (x | z) p (z)}{p (x)}] \\ = & E_{q} [\log q (z)] - E_{q} [\log p (x | z)] - E_{q} [\log p (z)] + E_{q} [\log p (x)] \\ = & - E_{q} [\log p (x | z)] + K L (q (z) | | p (z)) + E_{q} [\log p (x)] \end{aligned}$
最后结果里， $E_{q} [\log p (x)]$ 是一个常数（ $x$ 是已有的数据，所以 $\log p (x)$ 是常数）。前半部分 $- E_{q} [\log p (x | z)] + K L (q (z) | | p (z))$ 为证据下界（Evidence Lower Bound）,缩写为ELBO，那么整个公式可以改写为下面的样子。
$\begin{aligned} K L (q (z; θ) | | p (z | x))] \\ = & - E_{q} [\log p (x | z)] + K L (q (z) | | p (z)) + E_{q} [\log p (x)] \\ = & - E L B O + E_{q} [\log p (x)] \end{aligned}$
进一步，最小化KL散度，就是在最大化ELBO。因为 $E_{q} [\log p (x)]$ 是定值，而ELBO前面又有一个负号。所以式子可进一步改写成下面的样子。
$\begin{aligned} \arg min K L (q (z; θ) | | p (z | x))] \\ = & \arg max E L B O \\ = & \arg max E_{q} [\log p (x | z)] - K L (q (z) | | p (z)) \end{aligned}$
案例

假设我们有若干的数据 $x$ （不同颜色的点），我们需要从这些数据中推理出一个参数 $z$ ，那么就是在求最大后验估计 $p (z | x)$ 。假设我们有一个高斯混合模型 $q (z; θ)$ （灰色阴影），它假设数据是由多个高斯分布（也叫正态分布，即形如 $f (x) = \frac{1}{\sqrt{2 π σ^{2}}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}}$ ，其中 $μ$ 是均值， $σ^{2}$ 是方差的分布）混合而成。 $θ$ 包含了多个高斯分布的参数。

可以看到，随着迭代次数的增加， $q (z)$ 逐渐可以准确的拟合出不同颜色的点，也就是拟合出了 $q (z | x)$ 。

注意
尽管变分推断（VI）在运行速度上要比MCMC快，但是其需要先对后验分布进行一个假设，即其得到的近似解没有MCMC方法通过采样得到的近似解准确。

变分自编码器（Variational Auto - Encoder，VAE）

自编码器

输入层（蓝色的 $x$ ）和输出层(橙色的 $\hat{x}$ )具有相同的维度。 $z = e (x)$ 是一个降维后的隐藏层，其维度明显是小于输入层与输出层。

通过最小化输入数据和解码数据之间的重构误差（ $l o s s = | | x - \hat{x} | |^{2} = | | x - d (z) | |^{2} = | | x - d (e (x)) | |^{2}$ ）来学习参数。

相比较于PCA，自动编码器因深度神经网络所带来的非线性而具有更强的降维能力。

::: tips
提示
PCA降维后的向量是严格正交的。
:::

但是，要注意的一点是，在降维的时候应该尽量确保降维后的数据保存了尽可能多的原始数据信息。自编码器在隐藏层过于小或者编码器过于深的时候可能会导致因降维而丢失大量信息！所以要选择合适深度的编码器与合适尺寸的隐藏层。

此外，因为自编码器的训练是尽可能减小输入层和输出层之间的误差，所以其并不care降维后的隐藏层（维度对应了潜空间）是否有意义。这将导致从潜空间采样得到的点可能无法对应合理有意义的数据。当训练好后的自编码器用于测试集时，生成的数据可能会毫无意义（可以理解为过拟合于训练数据）。

VAE基本思想

此方案引入了正则化来避免过拟合，输入层经过编码后不再是点，而是概率分布。

图中的左列是用AE方案实现的结果，对应了笑的程度。右列是VAE方案的结果，也是对应了笑的程度，但是用概率分布来表达。

概率生成模型

p (z | x) = \frac{p (x | z) p (z)}{p (x)}

重温一下贝叶斯公式。AE的方案是在求MLE（最大似然估计）。而VAE方案是在求MAP（最大后验估计）。

在求 $p (z | x)$ 最大的时候实际上是在求 $p (x | z) p (z)$ 最大（因为 $p (x)$ 与 $z$ ）无关。所以进一步 $max p (z | x) = max p (x | z) p (z)$ 。为了方便计算，对 $p (x | z) p (z)$ 取对数，得到 $\ln p (x | z) p (z) = \ln p (x | z) + \ln p (z)$ 。当 $p (z)$ 为拉普拉斯分布概率密度函数时， $\ln p (z) = - l n (2 b) - \frac{| z |}{b}$ ，此时 $\ln p (z)$ 等价于引入了一个与 $| z |$ 相关的项。所以， $p (z)$ 可以理解为一个正则项，其用来避免过拟合。